Signalprocessing on the edge – µController basierte Radar Back-End Struktur 

Das FHR hat eine neue Back-End Struktur für eigene Radarsensoren entwickelt, die sich durch ihre Master / Slave Konfiguration zur Laufzeit abschalten, erweitern und umkonfigurieren lassen. Zusätzlich wurde die Signalverarbeitung durch Interpolation in der Art angepasst, dass diese direkt „on the edge“ auf dem µController durchgeführt werden kann. 

Das FHR fokussiert die Konzeptionierung verteilter Signalverarbeitungssyteme sowohl in der Verteilung energiesparender untereinander vernetzter Sensorik, als auch in der Konzepterstellung zur energieeffizienten Verteilung der Signalverarbeitung auf die Hardware und Softwarekomponenten über die Sensor-Edge-Cloud Komponenten hinweg. Ein hierzu im Projektverlauf zu realisierender, radarbasierter Beispielsdemonstrator wird einen vierkanaligen Radarsensor repräsentieren, der mit zwei µControllern ausgestattet wird. Diese µController basierten, vernetzten Sensorknoten und die zugehörige Firmware Entwicklung stellen die Hauptarbeiten des FHRs dar. Vier vernetzte phasenkohärente Radarknoten (80GHz/ 140 GHz) werden durch zwei vernetzte µController, welche in Master / Slave Konfiguration betrieben werden sollen, gesteuert und ausgelesen. Sowohl die Sensorknoten als auch der Slave-µController werden durch den Master-µController zu- bzw. abschaltbar sein. Die vier ADC-Kanäle sind ebenfalls konfigurierbar, sodass sowohl ein 1-4 Kanalbetrieb in der Standardabtastrate als auch ein 1-2-Kanalbetrieb im „Interleaved“ Mode für bis zu zwei Sensorknoten mit der doppelten Abtastrate unterstützt werden kann. 

Durch die Entwicklung neuer Back-End Strukturen, bei dem jede Platine einen µController enthält, wird das System weiter skalierbar. Dies bedeutet, dass nicht nur ein Slave-µController denkbar ist, sondern sich das System erweitern lässt. Für Szenarien, in denen mehr als vier Kanäle benötigt werden, lässt sich das Gesamtsystem um weitere Slave-µController erweitern. Die Entwicklung der Platine ist in Abbildung 1 und 2 festgehalten.

Für Entfernungsmessungen ist es notwendig, die einlaufenden Signale der Radarsensoren zu verarbeiten. Dabei bezieht sich die Verarbeitung hauptsächlich auf verschiedene Arten von reellen, komplexen und inversen Fourier-Transformationen.  Da die maximale Amplitude im Spektrum der resultierenden Zwischenfrequenz direkt korreliert mit der Entfernung zum Messobjekt, sind häufig große Blockgrößen der Fourier-Transformation nötig. Dies begründet sich durch den Auflösungsgrad der Frequenzschätzung im Spektrum, denn das Auflösungsvermögen ist Abhängig von der Abtastfrequenz und der gesamten Anzahl der Stützstellen im Spektrum. Auf µController Strukturen sind große Blockgrößen häufig wenig effizient implementierbar. Daher wurde ein Interpolationsverfahren gewählt, um das Auflösungsvermögen bei kleiner werdenden Blockgrößen äquivalent zu halten. Dieses Interpolationsverfahren basiert auf einer quadratischen Interpolation im Frequenzbereich. Eine einfache Verkleinerung der Blockgrößen würde zu Ungenauigkeiten in der Distanzbewertung führen. Daher ist es wichtig, Rechenleistung einzusparen allerdings bei gleichbleibender Genauigkeit. Ein weiterer Vorteil eines Interpolationsverfahrens begründet sich durch die Möglichkeit, die Frequenzschätzung im Spektrum nicht mehr diskret, sondern kontinuierlich durchzuführen.  

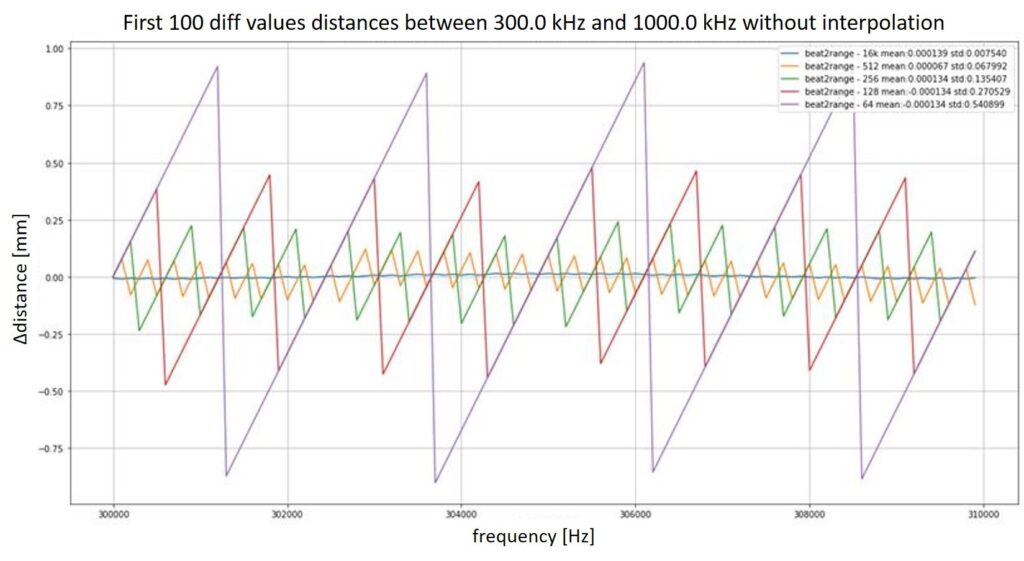
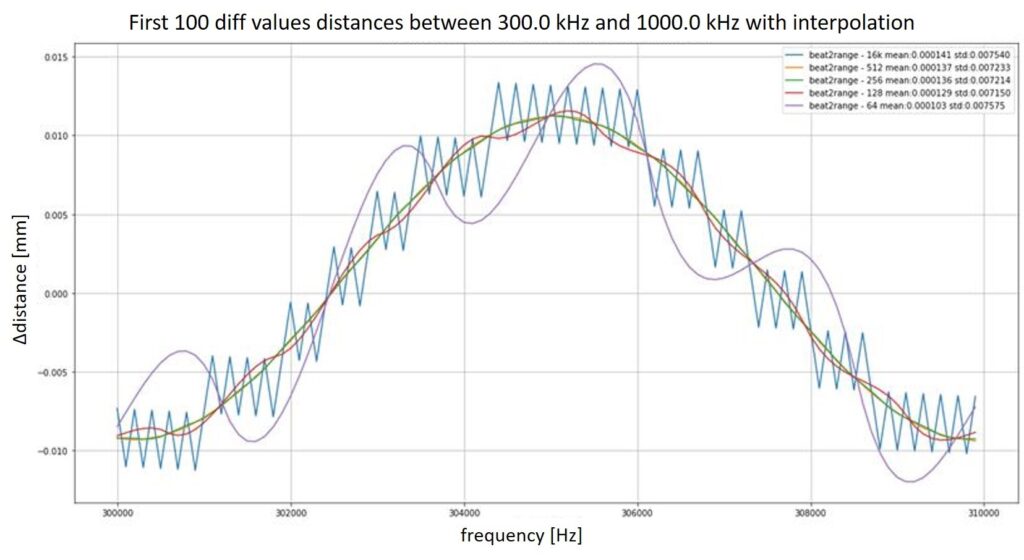
Um die gleichbleibende Genauigkeit zu validieren, wurden zwei Simulationen durchgeführt. Dabei bezieht sich die erste Simulation auf eine Überprüfung der einfachen Verkleinerung der Blockgröße ohne Interpolationsansatz (Abbildung 3). Abbildung 4 stellt die Ergebnisse einer Simulation mit Interpolationsansatz dar. Dabei zeigt sich, dass sich die Ergebnisse ohne Interpolation nicht verwerten lassen. Die Massgabe der gleichen Genauigkeit passt dabei nicht, da die Abweichung größer sind als bei einer Implemntierung mit einer 16k Fourier-Transformation.