The FHR has developed a new back-end structure for its radar sensors, which can be switched off, extended, and reconfigured at runtime by their master/slave configuration. In addition, signal processing by interpolation has been adapted so that it can be performed directly "on the edge" on the µController.

An article by Michel Andre Knieps, M.Sc.
Department Embedded Systems
Industrial High Frequency Systems Division (IHS)
Fraunhofer FHR
FHR focuses on the conceptual design of distributed signal processing systems both in the distribution of energy-efficient interconnected sensors, and in the conceptual design for energy-efficient distribution of signal processing to the hardware and software components across the sensor edge cloud components. A radar-based example demonstrator will be realized in the course of the project and will represent a four-channel radar sensor equipped with two µcontrollers. These µcontroller-based networked sensor nodes and the respective firmware development represent the main work of FHR. Four connected phase coherent radar nodes (80GHz/ 140 GHz) are controlled and scanned by two networked µcontrollers, which will be operated in master / slave configuration. Both the sensor nodes and the slave µcontroller will be able to be switched on and off by the master µcontroller. The four ADC channels are also configurable to support 1-4 channel operation in the standard sampling rate as well as 1-2 channel operation in "interleaved" mode for up to two sensor nodes at twice the sampling rate.
By developing new back-end structures, where each board contains a µcontroller, the system becomes further scalable. This means that not only a slave µcontroller is conceivable, but the system can be expanded. For scenarios where more than four channels are required, the overall system can be expanded with additional slave µcontrollers. The development of the board is shown in figure 1 and 2.


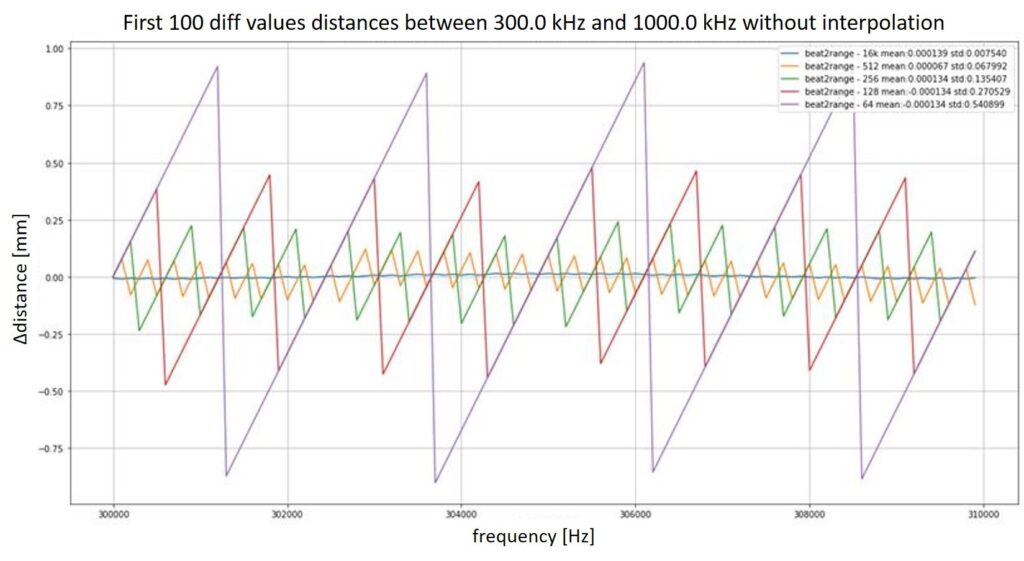
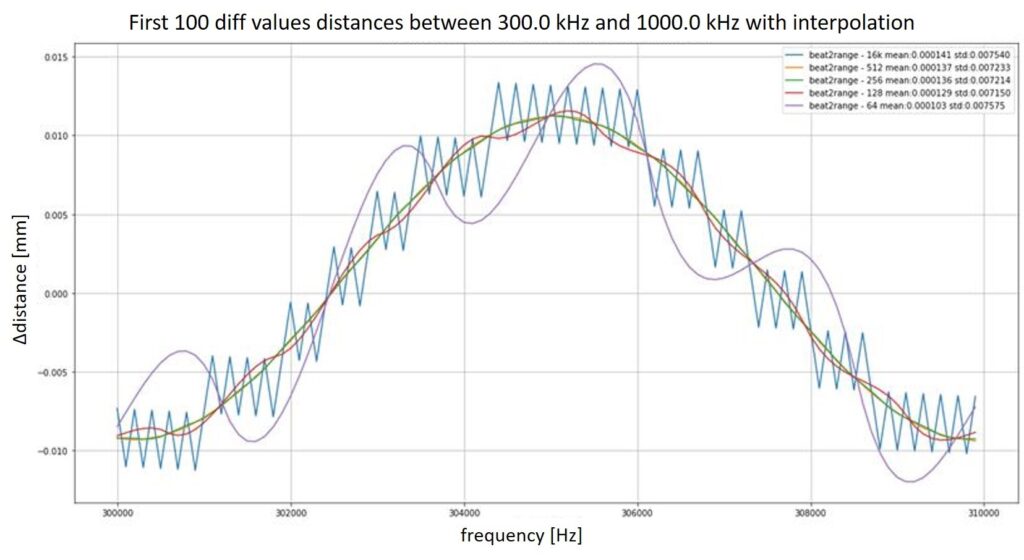
In order to measure distances, it is necessary to process the incoming signals from the radar sensors. The processing mainly refers to different types of real, complex, and inverse Fourier transforms. Since the maximum amplitude in the spectrum of the resulting intermediate frequency correlates directly with the distance to the measured object, large block sizes of the Fourier transform are often required. The reason for this is the degree of resolution for frequency estimation in the spectrum because the resolution capacity depends on the sampling frequency and the total number of interpolation points in the spectrum. On µController structures, large block sizes can often not be implemented efficiently. Therefore, an interpolation method keeps the resolving power equivalent with decreasing block sizes. This interpolation method is based on a quadratic interpolation in the frequency domain. A simple reduction of the block sizes would lead to inaccuracies concerning the distance evaluation. Thus, saving computing power while maintaining the same accuracy is important. Another advantage of an interpolation method is based on the possibility of performing the frequency estimation in the spectrum continuously instead of discretely.
Two simulations were performed to validate the consistent accuracy. The first simulation refers to verifying the simple reduction of the block size without the interpolation approach (Figure 3). Figure 4 presents the results of a simulation with an interpolation approach. It shows that the results without interpolation cannot be used. The measure of the same accuracy does not fit because the deviation is more significant than with an implementation with a 16k Fourier transform.